

Move3(aux,dest, src) And this is what we get when it is run Model.append(model.pop()) # move top disc on src to top of dest Print("move disk from %s to %s" % (src,dest))
We are going to avoid recursion by limiting the number of disks and writing a separate function for each case.Ĭode for hanoiNR.py model = ,] # A simple model, a list with 3 pegs each with up to 4 discs Here’s our first attempt at some control code. Done.Īnd with a 3-disc solution a 4-disc can be … I’m sure you have the idea. 2-disc to the auxillary peg, 1-disc to the destination and 2-disc again to move discs from the auxillary peg to the destination peg. Done.Īnd with that solution we can make a 3-disc solution. And finally move the disc on the auxillary peg to the destination peg.
#Hanoi towers visualzier code#
That can be done in a single statement.įor two discs (2-discs) we can invoke the 1-disc code three times: move the top (smallest) disc to the auxillary peg, then move the next to the destination peg. Pop it off the source peg and append it to the destination peg. If we need to move just one disc, it’s just a single step: move the disc from the source peg to the destination peg. We won’t bother with separate module for it.Īs we do in many of the projects, we want to start by finding a solution for the simplest case. That’s easy since it’s just a Python expression and the python print statement works fine. We’ll use the simple version of the model and the initial view will simply print the model. The control for the Tower of Hanoi will turn out be quite simple but tricky. At the start the model looks like the following with all discs stacked on the first peg (peg 0). The discs sorted by size top to bottom (small to large) on the peg. Each peg would also be a list with an integer for each disc. In this project we use a much simpler model, a list structure. Along with the attributes might be methods to move a disc from peg to peg and to calculate which disc and which peg should be next.īut this model would be fairly involved. A peg object might have attributes for its position and which disc objects are attached to it. Each disc might have attributes for its size and color along with which peg it is stacked. In the Tower of Hanoi an object oriented model might consist of a class for a disc and another for a peg. Some applications may have multiple views. The View outputs the model, either presenting a visual repretation, outputting information from the model, responding to signals from the Control or all of these. The Control is makes changes to the contents of the model and also passes the changing model along with other signals to the view.

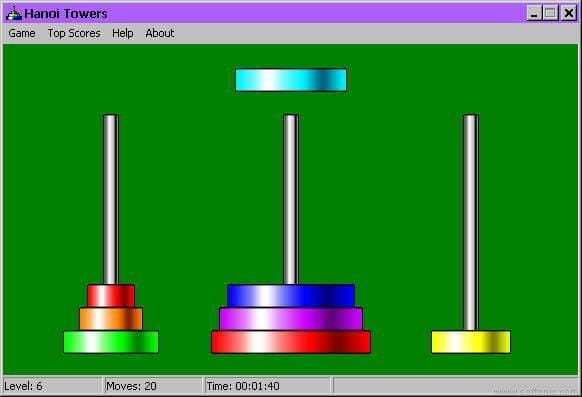
The Model is a structure for the data being manipulated by the program The MVC discipline strives to find separate responsibilities of a program into code modules that are independent and loosely linked with each other. And I think the problem is the difficulty in visualizing the nested context of the recursive calls. It is much better than the usual factorial example which does nothing more than use recursion to replace a simple for loop.īut students have a hard time getting it. I have tried a couple of times to teach the Hanoi puzzle as a good example of recursion. Here is a screen shot of the game in progress.Īnd here is a javascript animation. The other 99% of the program involves doing TK graphics to make it come alive. Guido's hanoi.py in the Python Demo area is a nice demonstration of this recursive process. Can't do 4 discs? Well then, move just 3.
#Hanoi towers visualzier how to#
If you don't know how to move 5 discs from A to C (using B for intermediate storage), then just move 4 discs from A to B, one disk from A to C (this is really easy) and then move 4 discs from B to C. The problem is to move the discs, one at a time from peg to peg in such a way that this is always true and to finally end up with all of the discs on peg 3 in the original order. A disc is never stacked on top of a smaller disc. In the initial configuration all the discs are stacked on the first peg with the largest disc on the bottom and the smallest on top. Each disc can fit on any of 3 pegs and each peg is high enough to hold all the discs in a stack. There are a number of discs each with a hole in the center. The Tower of Hanoi is a classic game that is often emulated on computers to demonstrate recursion.


 0 kommentar(er)
0 kommentar(er)
